Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyThe standard form of a quadratic function presents the function in the form latexf\left(x\right)=a{\left(xh\right)}^{2}k/latex where latex\left(h,\text{ }k\right)/latex is the vertex Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function The standard form is useful for determiningThis problem has been solved!

Ppt Graphs Of Quadratic Function Powerpoint Presentation Free Download Id
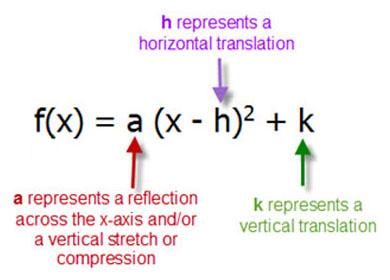
Transformations f(x)=a(x-h)^2+k
Transformations f(x)=a(x-h)^2+k-Analysing the given quadratic function f(x) = a(x−h)2k f (x) = a (x − h) 2 k is in standard form,we have (a) The graph of f is a parabola with vertex See full answer below Become a member Algebra what do the a, h, and k values do in the graphs of these functions??




3 Ways To Find The Maximum Or Minimum Value Of A Quadratic Function Easily
Find f(xh)f(x)/h f(x)=x^23x7 Consider the difference quotient formula Find the components of the definition Tap for more steps Evaluate the function at Tap for more steps Replace the variable with in the expression Simplify the result Tap for more steps Simplify each termConsider the graph of the parabola y=ax^2 Its vertex is clearly at (0,0) Now, if you replace x with xh in any equation, its graph gets shifted to the right by a distance of h> 5NumericalIntegration > 511 Simpson's rule The rule S 2(f) will be an accurate approximation to I(f) if f(x) is nearly quadratic on a,b For the other cases, proceed in
This video shows how to use horizontal and vertical shifts together to graph a radical functionQuestion Express f ( x) in the form a ( x − h) 2 k f (x) = − 3/4x 2 15x − 77Solution for Write the function in f(x) = a(x − h)2 k form Determine the vertex and the axis of symmetry of the graph of the function f(x) = 9x2 54x
Tema Funciones Cuadráticas f(x) = a(x – h)2 k Descripción Las funciones cuadráticas f(x) no siempre están en el formato a(x – h)2 k Para escribirlas así debemos completar el cuadrado Este formato es conveniente para el trazado de la gráfica, ya que podemos trasladarlas f(x) = a(x − h)2 k form Determine the vertex and the axis of symmetry of the graph of the function f(x) = x2 4x − 5Solution for f (x)=a (xh)2k equation Simplifying f (x) = a (x 1h) * 2 k Multiply f * x fx = a (x 1h) * 2 k Reorder the terms fx = a (1h x) * 2 k Reorder the terms for easier multiplication fx = 2a (1h x) k fx = (1h * 2a x * 2a) k fx = (2ah 2ax) k Solving fx =



2




3 Ways To Find The Maximum Or Minimum Value Of A Quadratic Function Easily
For the base function f (x) and a constant k > 0, the function given by g(x) = k f (x), can be sketched by vertically stretching f (x) by a factor of k if k > 1 or by vertically shrinking f (x) by a factor of k if 0 < k < 1 Horizontal Stretches and Shrinks For the base function f (x) and a constant k, where k > 0 and k ≠ 1, theF (x) = a*log (xh)k f (x) = a*2^ (xh) k i think the k is the horizontal asymptope butExplore the parent graph y=x^3 Experiment with the values of a, h, and k What happens to the graph as these values change?
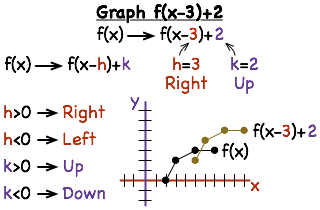



How Do You Graph A Translation Of A Function Printable Summary Virtual Nerd
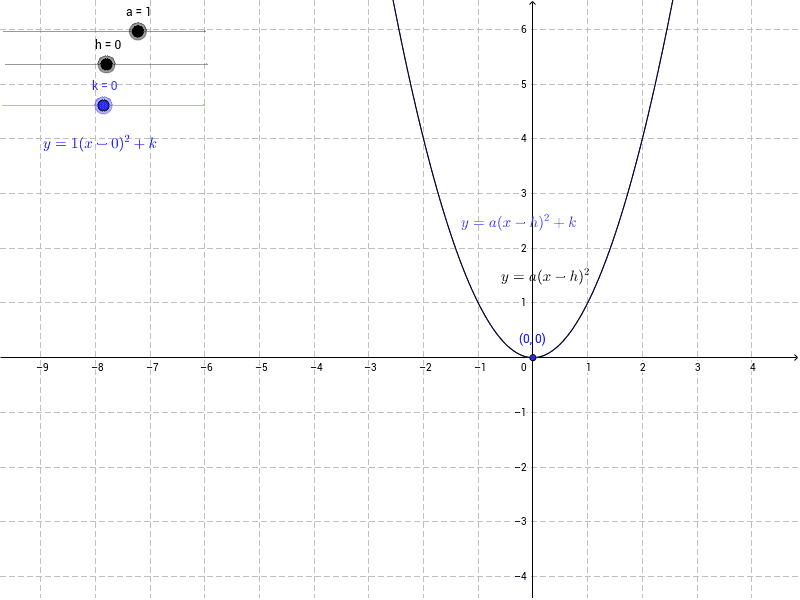



Investigating The Graph Of Y X H 2 K Geogebra
#h'(x)=f'(x)g(x)f(x)g'(x)# We are ask to find #h'(1)#, or by the product rule #h'(1)=f'(1)g(1)f(1)g'(1)# The values of the functions must be #f(1)=2# and #g(1)=4/3# Remember the derivative gives the slope of any given point, but as we can see in the figures these must correspond, to the slope of the line, which goes through theXk = X k x k!Graphing f (x) = a(x − h)2 k The vertex form of a quadratic function is f (x) = a(x − h)2 k, where a ≠ 0 The graph of f (x) = a(x − h)2 k is a translation h units horizontally and k units vertically of the graph of f (x) = ax2 The vertex of the graph of f (x) = a(x − h)2 k is (h, k), and the axis of symmetry is x = h h f(x) = ax2 y x f(x) = a(x − 2h) k k (h, k)




Quick Review Before Hw Quiz Y A X H 2 K Form Vertex H K Axis X H Up If A 0 Down If A 0 Ex Y X 1 2 4 Y 1 X 1 2 4 A 1
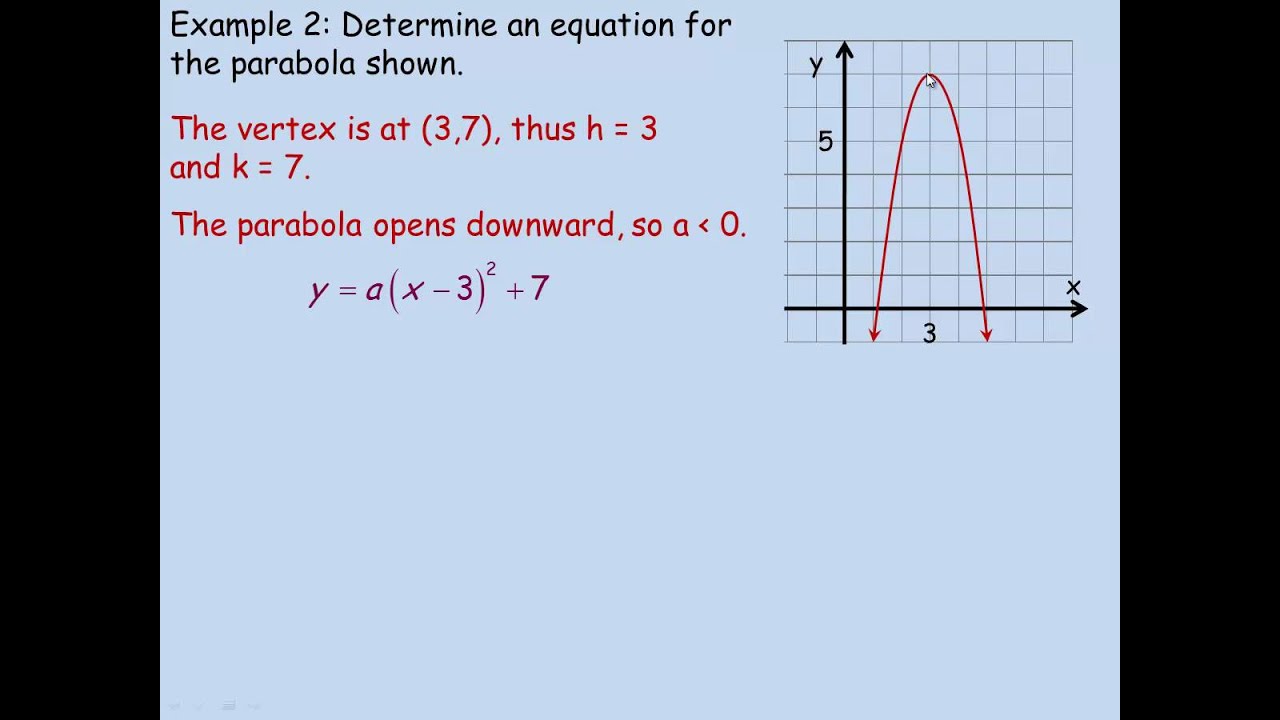



Graphing Y A X H K Youtube
1 P a g e Algebra 1 Unit 7 Exponential Functions Notes 1 Day 1 Transformations of Exponential Functions f(x) = a(b)xh k Describe the transformations of each variable in the tableWrite the function in the form $f(x)=a(xh)^{2}k$ by completing the square Then identify the vertex $$q(x)=2 x^{2}12 x11$$Let's start with an easy transformation y equals a times f of x plus k Here's an example y equals negative one half times the absolute value of x plus 3 Now first, you and I ide identify what parent graph is being transformed and here it's the function f of x equals the absolute value of x And so it helps to remember what the shape of that




Pre Calculus 2 6a Page 160 S 1 23odd Ppt Video Online Download




Vce Mathematical Methods Units 1 And 2 4g Graphing Quadratic Functions
I will answer this way, since I suspect you're preparing for finals The x and y are the variables They aren't replaced with specific numbers in the equation unless you are finding (x, y) coordinates for points on the parabola The h is a horizonF(x) = a(x h) 2 k The a in the vertex form of a parabola corresponds to the a in standard form If a is positive, the parabola will open upwards If a is negative, the parabola will open downwards In vertex form, (h,k) describes the vertex of the parabola and the parabola has a line of symmetry x = h(a) For any constant k and any number c, lim x→c k = k (b) For any number c, lim x→c x = c THEOREM 1 Let f D → R and let c be an accumulation point of D Then lim x→c f(x)=L if and only if for every sequence {sn} in D such that sn → c, sn 6=c for all n, f(sn) → L Proof Suppose that lim x→c f(x)=LLet {sn} be a sequence in D which converges toc, sn 6=c for all nLet >0




Ppt Quadratics Of The Form Y A X H 2 K Powerpoint Presentation Id




Unit 5 Quadratic Functions Flashcards Quizlet
That is, h is the xcoordinate of the axis of symmetry (ie the axis of symmetry has equation x = h), and k is the minimum value (or maximum value, if a < 0) of the quadratic function One way to see this is to note that the graph of the function ƒ ( x ) = x 2The highest point is the vertex If x1 and x2 are the x intercepts of the graph then the x coordinate h of the vertex is given by (see formula above) h = (x1 x2) / 2 = ( 4 6) / 2 = 1 We now know the x (h = 1) and y coordinates (k = 6) of the vertex which is a point on the graph of the parabola Hence fVertex (1,2) yintercept (0,1) xintercept , 015 Explanation y = a ⋅ (x − h) 2 k is the equation of parabola, with vertex (h,k) y = 3 x 2 6 x 1 = 3 ⋅ ( x 2 2 x 1 ) − 2




F X X H 2 K Prepared By Ansiluz H Betco San Bartolome High School Pptx Powerpoint




The Following Graph Of F X X2 Has Been Shifted Into The Form F X X H 2 K Brainly Com
A polynomial function in one variable of degree 2 Polynomial form f(x)= a 2 x 2 a 1 x a 0 Standard form 1 f(x) = ax 2 bx c Standard form 2 f(x) = a (xh) 2 k Cubic function A polynomial function in one variable of degree 3 Polynomial form f(x)= a 3 x 3 a 2 x 2 a 1 x a 0 Quartic function A polynomial function in oneSpanish2B Chapter 46 Vocabulary Words 214 terms Claire_Marie8 x=a (yk)^2h 7 terms Claire_Marie8 1450present 35 terms Claire_Marie8X k ∆kf(a) k!



1




Chapter 3 1 Quadratic Functions And Models Example
Express f (x) in the form a (x − h)2 k f (x) = − 3/4x2 15x − 77 f (x)=?For instance, when D is applied to the square function, x ↦ x 2, D outputs the doubling function x ↦ 2x, which we named f(x) This output function can then be evaluated to get f(1) = 2, f(2) = 4, and so on Higher derivatives Let f be a differentiable function, and let f ′ be its derivativeA quadratic function is a polynomial function of degree two The graph of a quadratic function is a parabola The general form of a quadratic function is f(x) = ax2 bx c where a, b, and c are real numbers and a ≠ 0 The standard form of a quadratic function is f(x) = a(x − h)2 k where a ≠ 0



Index Of Ojj Rcm27 Images
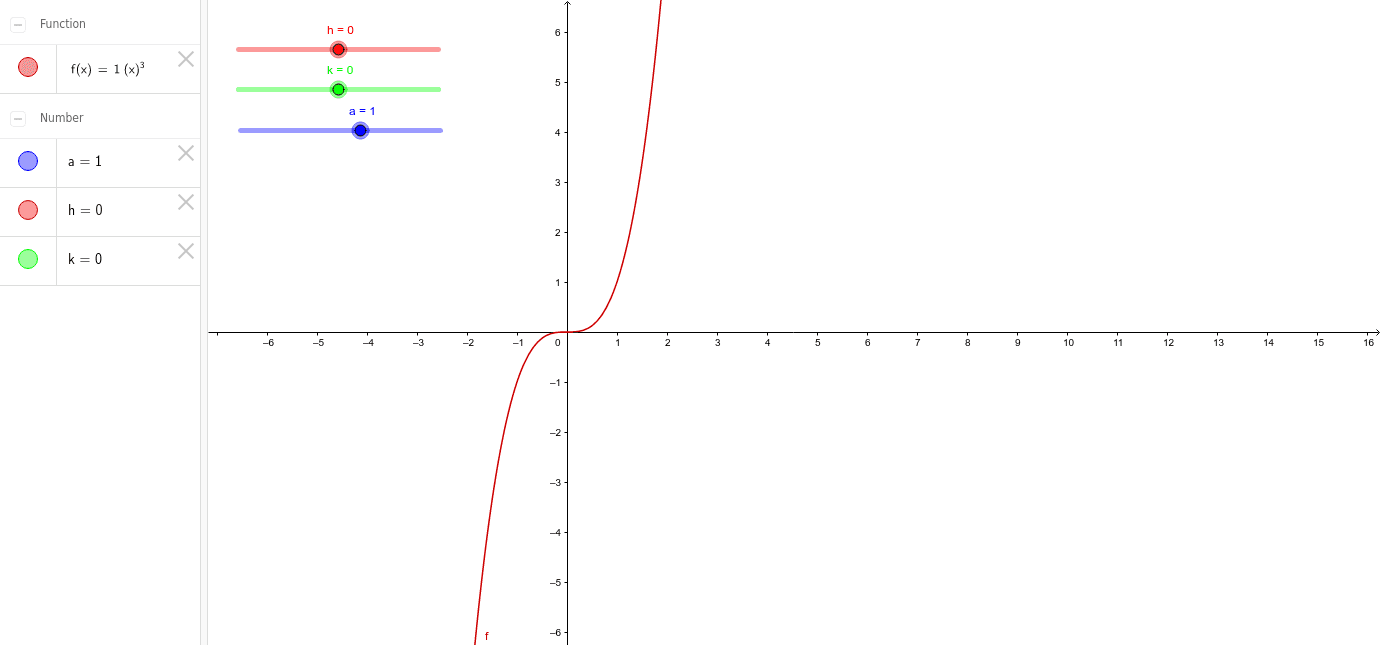



Y A X H 3 K Geogebra
2 x 1 = f(x 2) f(x 1) x 2 x 1 (61) It's a linear approximation of the behavior of f between the points x 1 and x 2 7 Quadratic Functions The quadratic function (aka the parabola function or the square function) f(x) = ax2 bx c (71) can always be written in the form f(x) = a(x h)2 k (72) where V = (h;k) is the coordinate of the vertexFor a function f (x), the difference quotient would be f(xh) f(x) / h, where h is the point difference and f(xh) f(x) is the function difference The difference quotient formula helps to determine the slope for the curved lines The f(xh) f(x) / h calculator can be used to find the slope value, when working with curved linesProofLet fK g 2A be a family of convex sets, and let K = \ 2AK Then, for any x;y2 K by de nition of the intersection of a family of sets, x;y2 K for all 2 nd each of these sets is convex Hence for any 2 A;and 2 0;1;(1 )x y2 K
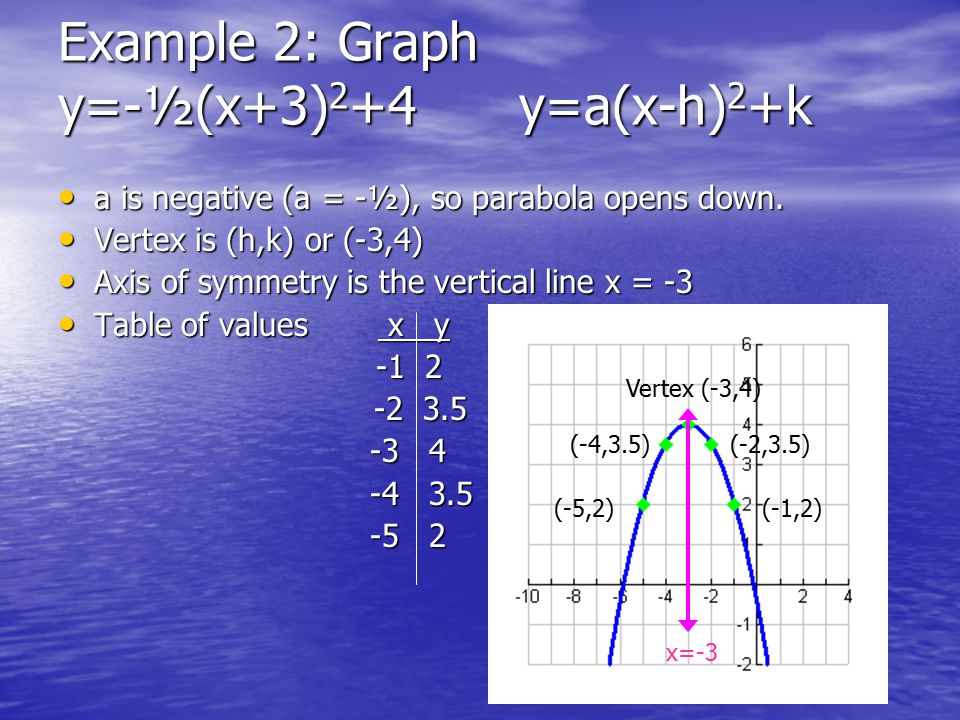



1 2 Graphing Quadratic Functions In Vertex Or Intercept Form Ppt Video Online Download




Functions In Standard Form Pdf Free Download
F(x)=a(xh)^2k (vertex form of equation for a parabola) Then, give the vertex of its graph f(x)=−2x^212x *** −2x^212x complete the square f(x)=2(x^26x9)18 f(x)=2(x3)^22 This is an equation of a parabola that opens down with vertex at (3,2)The submatrix H i, j is of dimension P 2 × P 2 and represents the contribution of the jth band of the input to the ith band of the output Since an optical system does not modify the frequency of an optical signal, H will be block diagonal There are cases, eg, imaging using color filter arrays, where the diagonal assumption does not hold Substitute ah and a for x in the formula for f(x) and simplify to find (f(ah)f(a))/h = 2a 2 h >f(x) = x^22x3 Then (f(ah) f(a))/h =(((ah)^22(ah)3



Applying Quadratic Models Mapa Mental




Write The Quadratic Function In F X A X H 2 K Form Whose Graph Is Shown F X Brainly Com
Transform of f(x) = 2 x Back Exponential Functions Function Institute Mathematics Contents Index Home This program demonstrates several transforms of the function f(x) = 2 xYou can assign different values to a, b, h, and k and watch how these changes affect the shape of the graphFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorSee the answer The quadratic function f (x) = a (x − h)2 k is in standard form (a) The graph of f is a parabola with vertex (x, y) = (b) If a > 0, the graph of f opens In this case f (h) = k is the value of f (c) If a < 0, the graph of f opens In this case f (h) = k




Funcion Cuadratica De La Forma X H 2 K Geogebra




Graph F X X H 2 Youtube
F (x) = a(x h) 2 k, where (h, k) is the vertex of the parabola FYI Different textbooks have different interpretations of the reference " standard form " of a quadratic function Some say f ( x ) = ax 2 bx c is "standard form", while others say that f ( x ) = a ( x h ) 2 k is "standard form"10 5 Sketch the graph of the function f(x) = x 2 (x–2)(x 1) Label all intercepts with their coordinates, and describe the "end behavior" of f That f(x) is a 4thdegree POLYNOMIAL* function is clear without computing f(x) = x4 – x3 – 2x2 f(x) = x2 (x–2)(x 1) v v The ROOTS of f are 0,0, 2Write the quadratic function in the form f (x)= a (x h)^2 k Then, give the vertex of its graph f (x)= 2x^2 4x 4 Studycom Math General Mathematics Quadratic functions Write the




Quadratic Functions



Solution The Graph Of F X X H K Contains The Points 6 2 And 0 2 The Graph Has A Vertex At H 5 Describe How To Find The Value Of H Then Explain How This Value Translates
∆kf(a) = f(ax) real a,x difference formula f = polynomial 9 Euler's summation X a≤k66E 67E The quadratic function f ( x) = a ( x − h)2 k is in standard form ( a) The graph of f is a parabola with vertex (____, ____) (b) If a > 0, the graph of f opens ________ In this case f ( h) = k is the _______ value of f (c) If a < 0, the graph of f opens




Mm2a3 Students Will Analyze Quadratic Functions In The Forms F X Ax 2 Bx C And F X A X H 2 K Mm2a4b Find Real And Complex Solutions Of Equations Ppt Download
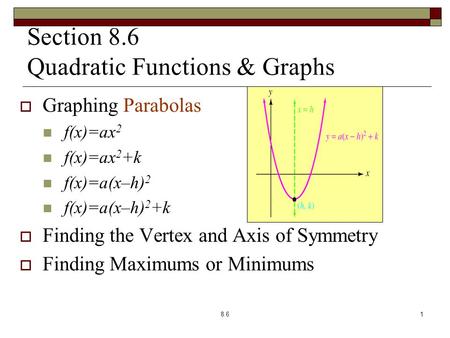



Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21
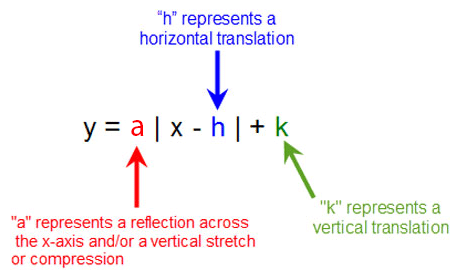



Untitled Document



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora



Staffweb Psdschools Org Eharding Alg1v Bigideasch 8 A1v8 4notesgraphingf A Xh K Pdf




Transforming Quadratic Functions From General Form To Standard Form




Write The Quadratic Function In The Form G X Chegg Com
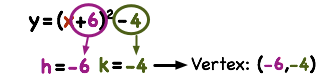



How Do You Convert A Quadratic From Standard Form To Vertex Form By Completing The Square Printable Summary Virtual Nerd




How To Graph A Quadratic Equation 10 Steps With Pictures
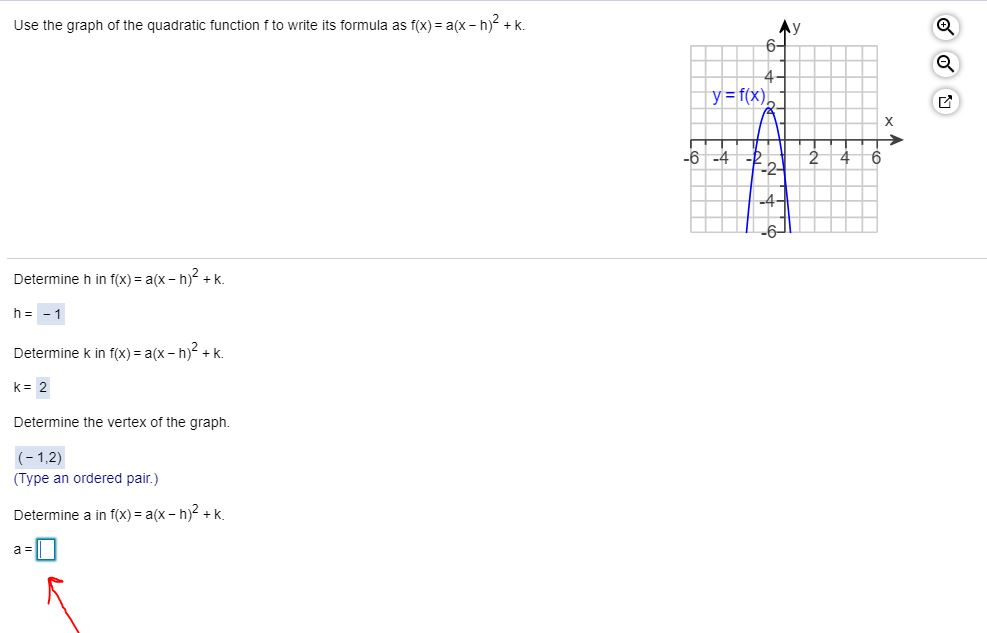



Use The Graph Of The Quadratic Function F To Write Chegg Com



Untitled Document
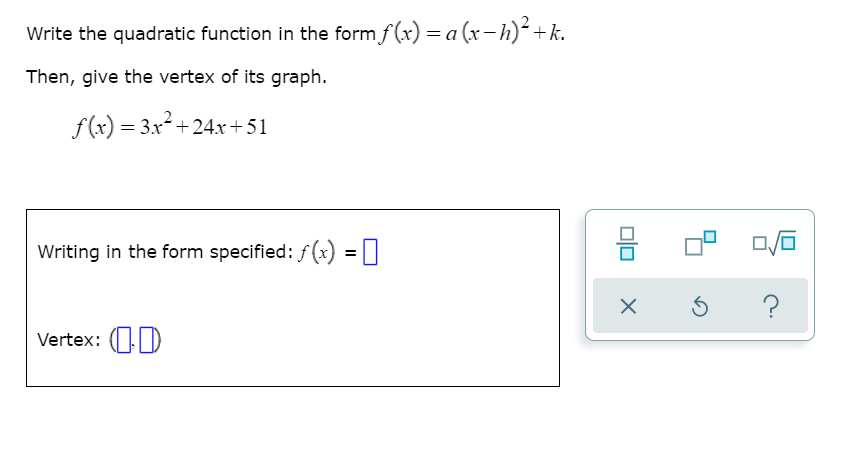



Answered Write The Quadratic Function In The Bartleby



1




2 4 Quadratic Functions Ppt Download




Calgebra A1 8 4 Graphing F X A X H 2 K Youtube




Ppt Graphs Of Quadratic Function Powerpoint Presentation Free Download Id




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube




Transform The Following Quadratic Functions In The Form F X A X H 2 K Determine The Values Of A H Brainly Ph




The Vertex Form Of A Quadratic Function Is F X A X H 2 K What Is The Vertex Of Each Function Brainly Com




Lesson Effects Of Changing A H And K In The Graph Of Quadratic Functi



Write The Quadratic Function F X X2 2x 6 In The Form F X A X H 2 K By Completing The Square And Ii Graph The Function Submit Graph Need Enotes Com
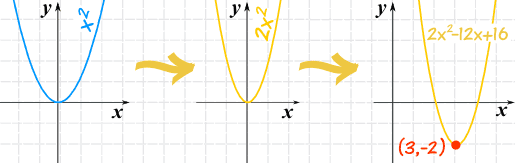



Graphing Quadratic Equations




6 6 Analyzing Graphs Of Quadratic Functions



Solved Use The Graph Of The Quadratic Function F X A X H 2 K To Find The Vertex Axis Of Symmetry And The Minimum Or Maximum Value Of The Functi Course Hero




Vertex Form Introduction Video Khan Academy



When You Use The Vertex Form Y A X H 2 K What Information Do You Get From A Vertex Form Quora
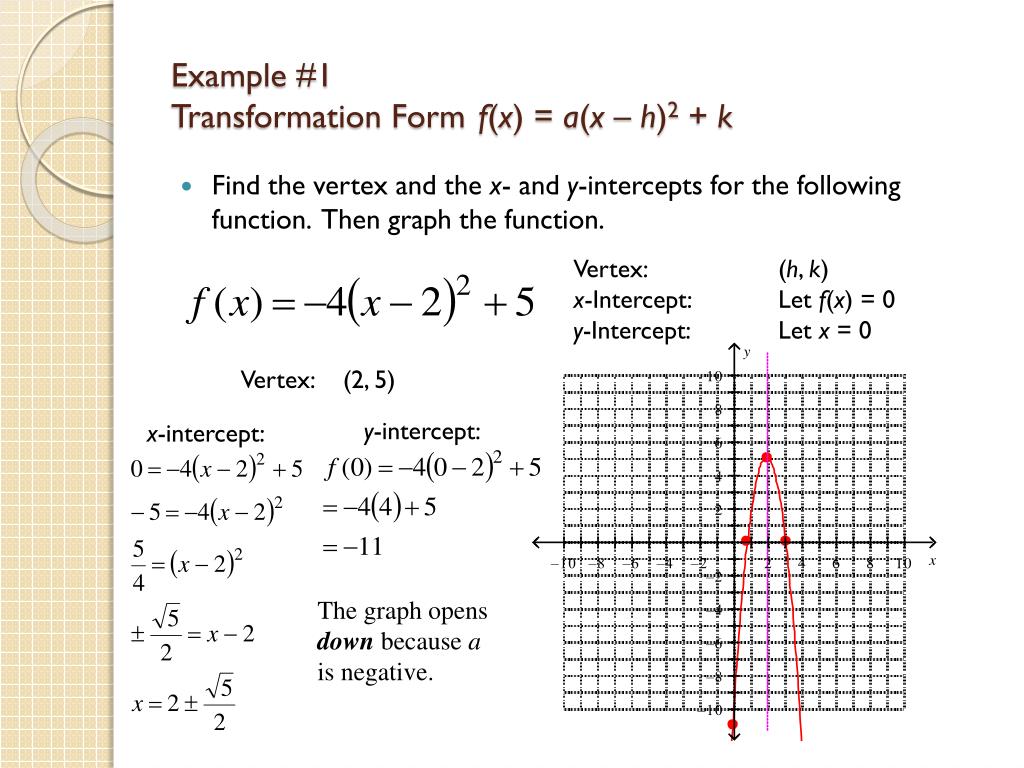



Ppt 3 3 Quadratic Functions Powerpoint Presentation Free Download Id




Section 5 3 Transforming Parabolas Standard Form Vs Vertex Form Standard Form Is Y Ax 2 Bx C Vertex Form Is Y A X H 2 K Ppt Download
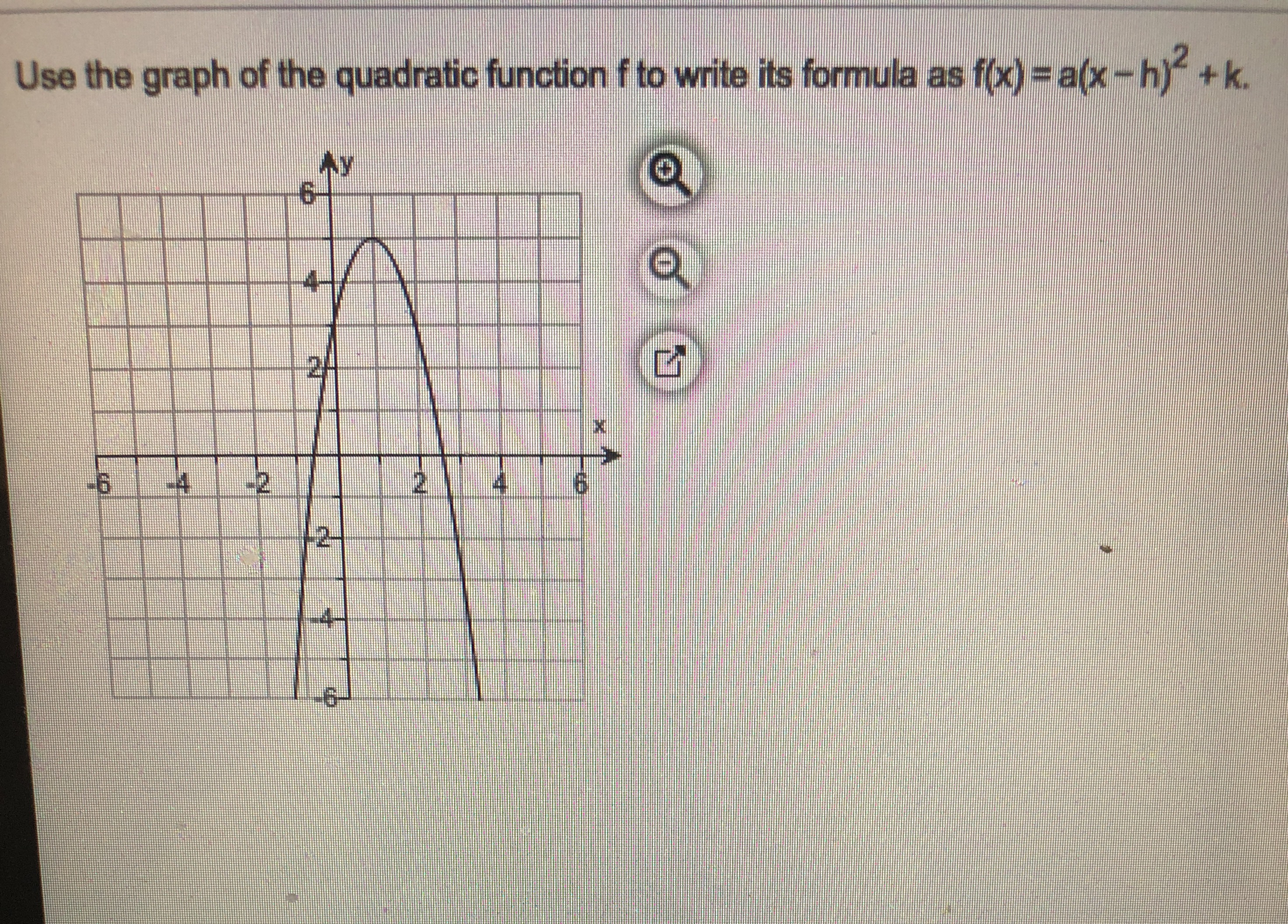



Answered Use The Graph Of The Quadratic Function Bartleby



Math Spoken Here About Quadratics 3



Grafica De Y A Y H 2 K Algebra



Solved Use The Graph Of A Quadratic Function F To Write Its Formula As F X A X H 2 K F X Course Hero




Write The Quadratic Function In The Form F X Chegg Com




Explaining A And H When You Have Y A X H 2 Youtube




Determine The Quadratic Function Of The Form F X Chegg Com




How To Write Quadratic Functions Video Lesson Transcript Study Com
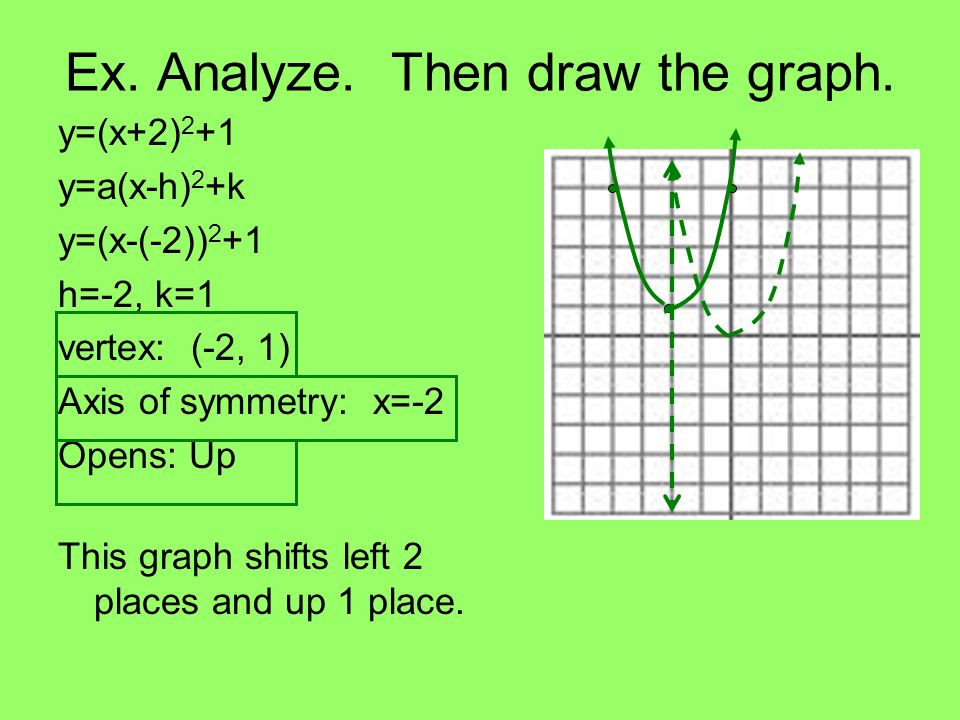



6 6 Analyzing Graphs Of Quadratic Functions Ppt Download
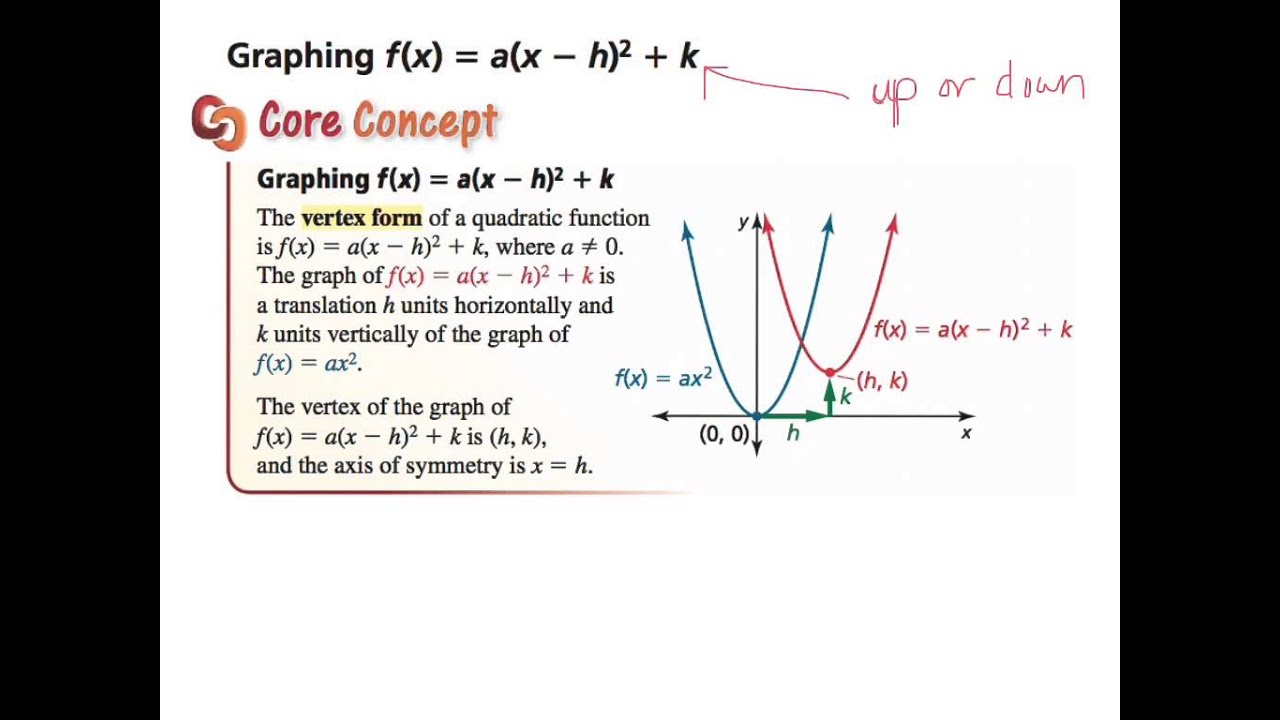



7th Section 8 4 Graphing F X A X H 2 K Youtube




Algebra Ii 9 5a Graphs Of F X A X H K Guidelines For Graphing Quadratic Functions Youtube




Quadratic Functions




The Graph Of F X X 2 Has Been Shifted Into The Form F X X H 2 K What Is The Value Of H A 1 B Brainly Com




The Axis Of Symmetry Is X H This Is The Vertical Line That Passes Through The Vertex 3 1 Quadratic Functions And Application Quadratic Functions Ppt Download




Answered Use The Graph Of The Quadratic Function Bartleby



Review Melody Davis And Jessica Perry




Solved For F X A X H 2 K In What Quadrant Is



Solved The Graph Shows G X Which Is A Translation Of F X X 2 Write The Function Rule For G X Write The Answer In The Form A X H 2 K Course Hero




Mathematics Learners Material Module 2 Q



Solution Write The Quadratic Function In The Form F X A X H 2 K Find The Vertex And Graph The Function A F X X 2 6x B F X X 2 4x 1 C F X 3x 2 10x 2




8 4 Graphing F X A X H 2 K Youtube




Rewrite The Following Quadratic Functions In Chegg Com




Describe The Graph Of F X A X H 2 K When A 0 Is The Graph The Same As That Of G X Ax 2 Bx C When A 0 Explain Study Com




Quadratic Functions



Solved Use The Vertex H K And The Point On The Graph Xy To Find The Standard Form F X A X H 2 K Of This Equation Quadratic Function Course Hero




Answered Create A New Function In The Form Y Bartleby



1




Quadratic Functions




Graphing A Parabola In The Form Y X H 2 K Youtube
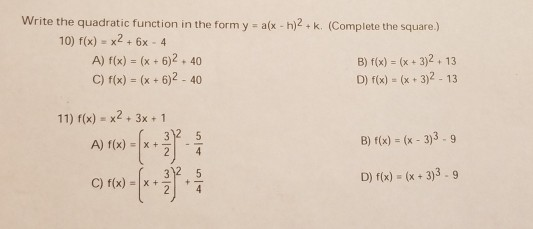



Write The Quadratic Function In The Form Y A X H 2 K Chegg Com




U4 2 5 Funcion De La Forma F X A X H 2 K Parte 2 Youtube



Sections 6 And 8 Quadratics Part 2 And Polynomial Functions




Quadratic Function Formulas Definition Graphs Examples




Ch 7 Tutoring Notes Quadratics
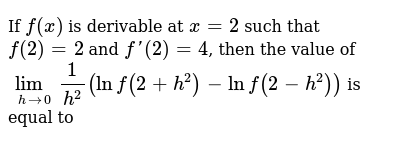



The Graph Of F X X2 Has Been Shifted Into The Form F X X




Quadratic Functions Ppt Download



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




Quadratic Formula Calculator




Standard Form To Vertex Form Without Completing The Square Method Algebra 2 Youtube




Quadratic Functions And Models Ppt Video Online Download




Finding Features Of Quadratic Functions Video Khan Academy




I Need To Write The Given Function In The Form Of Chegg Com
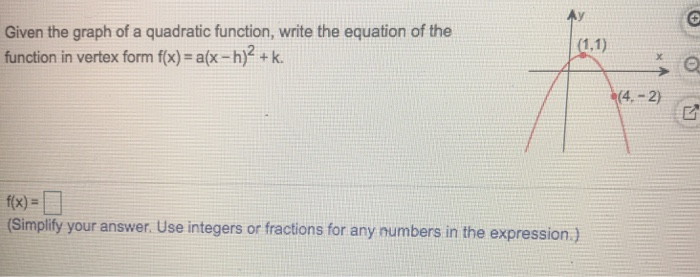



Given The Graph Of A Quadratic Function Write The Chegg Com
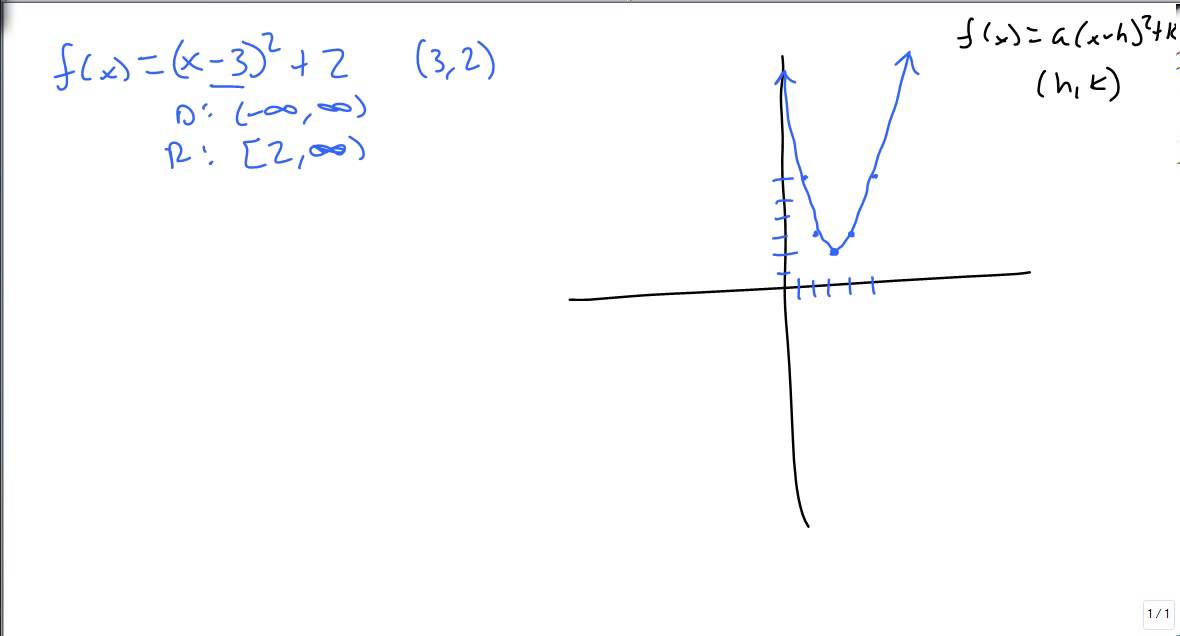



Graph By Transformations F X A X H 2 K Youtube



Quadratic Function




Quadratic Functions




Quadratic Function Wikipedia




3 Manieres De Trouver Facilement Les Valeurs Maximale Et Minimale D Une Fonction Du Second Degre



Quadratic Functions In The Form Y A X H 2 K Ppt Download
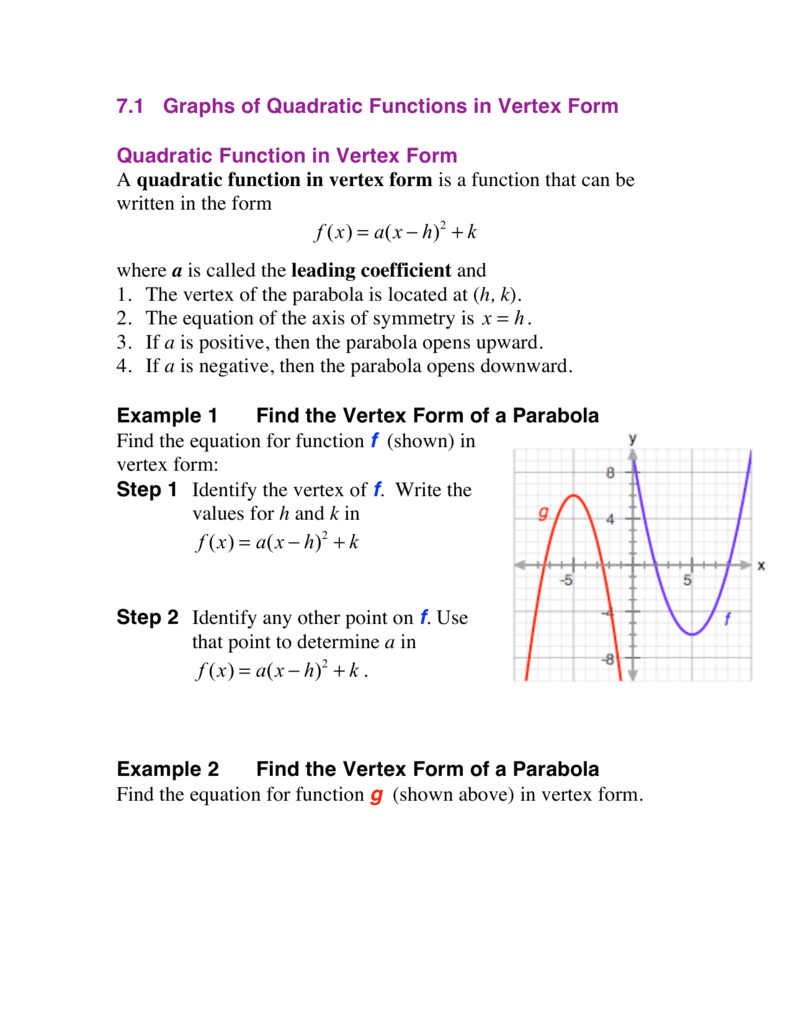



F X A X H 2 K F X A X H 2 K F X A X H 2 K
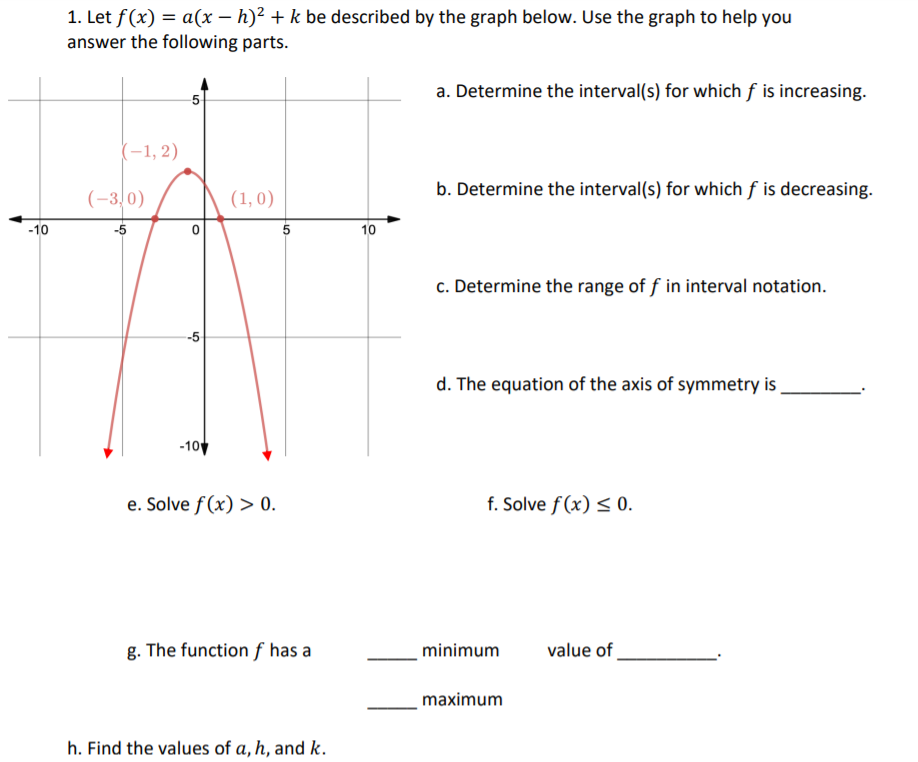



Let F X A X H 2 K Be Described By The Graph Below Chegg Com



0 件のコメント:
コメントを投稿